Ученый НИУ ВШЭ оптимизировал решение задачи по гидродинамике

Доцент департамента прикладной математики МИЭМ НИУ ВШЭ Роман Гайдуков смоделировал движение жидкости вокруг вращающегося диска с малыми неровностями. Разработка делает возможным предсказание поведения потока жидкости без мощных суперкомпьютеров. Результаты опубликованы в журнале Russian Journal of Mathematical Physics.
Гидродинамика изучает движение жидкостей и их взаимодействие с твердыми поверхностями. Этот раздел физики позволяет понять и прогнозировать, как жидкости и газы будут вести себя в различных условиях. В том числе принципы гидродинамики используются в электрохимии при расчетах реакций гальванизации (молекулы серебра прилипают к металлической детали) и окисления (формирование патины на меди).
В этих процессах используется дисковый электрод — плоская металлическая пластина, вращающаяся в жидкости. Для расчета электрохимических реакций необходимо знать, как именно жидкость будет двигаться вокруг электрода и какие условия нужно соблюдать. Для этого ученым приходится рассчитывать множество переменных. Даже небольшие неровности на поверхности диска могут существенно влиять на течение жидкости, создавая сложные и неожиданные эффекты.
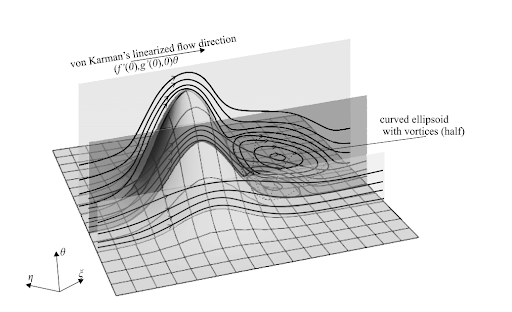
Ранее исследования касались только симметричных неровностей, ученый из НИУ ВШЭ рассмотрел более сложный случай. Роман Гайдуков рассчитал, как изменится поток жидкости, если на поверхности вращающегося диска встречаются асимметричные неровности.
Для этого он использовал метод многопалубных структур пограничного слоя, который позволил разложить трехмерную задачу на серию двухмерных. Метод помогает решать сложные задачи гидродинамики при высоких значениях числа Рейнольдса, когда прямое моделирование невозможно. Хотя этот метод известен с конца 1960-х годов, строгая математическая формулировка была разработана автором статьи совместно с профессором Владимиром Даниловым не так давно. Математический алгоритм метода может быть интегрирован в любой математический пакет символьных вычислений.

Роман Гайдуков
«В реальных условиях абсолютно гладких поверхностей не бывает. Мы показали, как небольшие неровности на поверхности диска влияют на поток жидкости, образуя зоны с вихрями и изменяя структуру пограничного слоя, — объясняет Роман Гайдуков. — Наш метод позволяет моделировать задачу за несколько часов, тогда как на суперкомпьютере это могло бы занять дни или даже недели. Это не только экономит время, но и снижает затраты на вычислительные ресурсы. Метод эффективно работает при больших, но конечных числах Рейнольдса».
Число Рейнольдса — это безразмерное число, описывающее соотношение между инерционными и вязкими силами в потоке жидкости. Большое число Рейнольдса указывает на преобладание инерционных сил, что приводит в том числе к турбулентным (хаотическим) потокам, а малое — на преобладание вязких сил, что приводит к ламинарным (упорядоченным) потокам.
Разработанный подход может использоваться для точного моделирования процессов движения жидкостей в ходе химических реакций, что может найти широкое применение в промышленности.
В будущем ученый планирует расширить свои исследования на более сложные системы, включающие взаимодействие различных фаз — например, капель жидкости в потоке воздуха или аэрозолей. Это позволит еще глубже понять процессы, происходящие в многокомпонентных и многофазных системах, и улучшить существующие модели.
Роман Гайдуков добавляет: «Мы с моим аспирантом Никитой Буровым планируем изучить, как изменяется форма капель жидкости на поверхности при обтекании их потоком воздуха и как одновременно сама капля как неровность влияет на этот поток, в том числе с учетом возможного замерзания капли».
