Парные перескоки частиц удержали жидкость Латтинжера от перехода в фазу локализации в беспорядке

Это еще один шаг к созданию квантового компьютера. Ученые из Российского квантового центра, НИУ ВШЭ и МФТИ изучили фазовый переход в одномерных системах с беспорядком в присутствии коррелированного перескока частиц. Работа была опубликована в Physical Review Journals. Она открывает возможности для создания устойчивых одномерных атомных ловушек, квантовых нитей, кристаллов с одномерной проводимостью.
В одномерных проводниках, таких как квантовые провода, взаимодействие электронов проявляется совершенно иным образом, чем в более привычных трехмерных и двумерных системах. В трехмерной среде поведение электронов хорошо описывается теорией Ферми-жидкости, основанной на модели Ферми-газа, которая предполагает слабое взаимодействие между частицами. В приближениях классической физики электроны в проводнике часто рассматриваются как идеальный газ.
Однако в одномерных системах ситуация значительно усложняется. Здесь проявляются уникальные особенности, связанные с квантовыми эффектами и сильным взаимодействием между частицами. Для анализа таких систем ученые применяют теорию жидкости Латтинжера (или Томонаги — Латтинжера). Эта теория описывает низкоэнергетические возбуждения в электронном газе как взаимодействие бозонов, что позволяет эффективно моделировать коллективные явления, такие как квазичастицы Латтинжера. Эти квазичастицы возникают благодаря корреляциям между электронами в узких одномерных структурах.
Ключевым аспектом теории Латтинжера является то, что электроны могут проявлять коллективное поведение, схожее с поведением бозонов на низких энергиях, — это происходит за счет квантовых флуктуаций. Эта уникальная характеристика позволяет исследовать такие явления, как фазовые переходы, и другие коллективные эффекты, которые невозможно объяснить традиционными моделями.
Для создания и эксплуатации углеродных нанотрубок, квантовых проводов, атомных ловушек и тому подобных одномерных квантовых систем важно удерживать жидкость Латтинжера от фазового перехода в локализованное состояние в присутствии беспорядка. Для этого необходимо исследование условий, при которых происходит этот фазовый переход.
В своей работе российские физики изучили, как интенсивность парных перескоков частиц (одновременного обмена местами пар частиц в цепочке) в одномерной цепочке влияет на сохранение делокализованного состояния жидкости Латтинжера. Большое количество таких прыжков характерно для высокого уровня квантовых корреляций между частицами, и, следовательно, в объеме одномерной системы доминируют сверхпроводящие корреляции. Они приводят, как правило, к формированию коллективного поведения в квантовой системе.
Ученым удалось показать, что если парные корреляции и прыжки достаточно сильные, то жидкость Латтинжера сохраняется лишь при достаточно высокой упорядоченности расположения частиц (слабом беспорядке). Но если они расположены весьма хаотично (беспорядок достаточно сильный), то происходит фазовый переход в локализованную фазу Бозе-стекла.
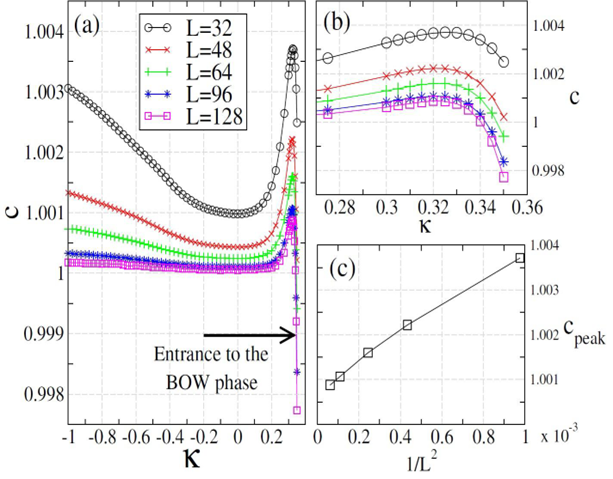
Для расчетов ученые использовали разные значения параметра ![]() , равного отношению количества парных прыжков к количеству одиночных прыжков. В зависимости от преимущественного направления этих прыжков параметр может иметь знак минус или плюс. Расчеты проводились для систем различных размеров.
, равного отношению количества парных прыжков к количеству одиночных прыжков. В зависимости от преимущественного направления этих прыжков параметр может иметь знак минус или плюс. Расчеты проводились для систем различных размеров.
Сначала было исследовано, как ведет себя центральный заряд одномерной системы частиц в чистой системе. Оказалось, что если доля парных прыжков частиц по отношению к одиночным прыжкам превышает одну треть, то наблюдается переход в особое неустойчивое состояние, которое происходит по механизму Березинского — Костерлица — Таулесса.
Затем ученые построили фазовую диаграмму, которая показывает, при каких уровнях беспорядка и доле парных прыжков частиц наблюдаются фазы жидкости Латтинжера, Бозе-стекла и неустойчивого состояния.
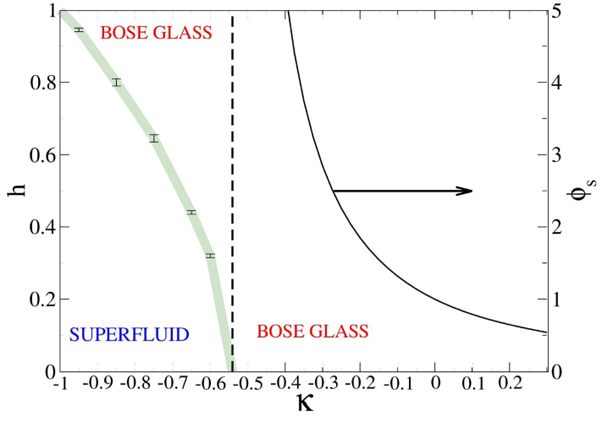
Оказалось, что если парные прыжки достаточно частые и происходят в направлении, противоположном одиночным прыжкам, то может наблюдаться состояние жидкости Латтинжера. Если парные прыжки достаточно редки, то реализуется только фаза Бозе-стекла. А если парные прыжки происходят часто и в том же направлении, что и одиночные прыжки, то наблюдается особое неустойчивое состояние.

Мурод Баховадинов
«Результаты нашего исследования могут быть применены для защиты квантовых состояний от декогеренции, что крайне важно для создания квантового компьютера. Упорядоченность расположения частиц в одномерной системе при достаточно сильных квантовых корреляциях между частицами позволяет сохранить сверхтекучее состояние квантового провода», — объясняет первый автор статьи, аспирант базовой кафедры физики конденсированных сред ИФТТ РАН факультета физики НИУ ВШЭ, научный сотрудник РКЦ Мурод Баховадинов.
